Rumus Phytagoras adalah rumus yang sering di pakai dalam pelajaran matematika di sekolah. Kadang kita di buat bingung dengan rumus pitagoras matematika, bagaimana cara membuktikan kebenarannya? Kurang lebih uraian tentang rumus phytagoras seperti di bawah ini.
Rumus asli phytagoras
Membuktikan kebenarannya, di mulai dengan membuat gambar sebuah persegi besar, kemudian gambarlah sebuah persegi kecil di dalam persegi besar tersebut, seperti gambar berikut:
Perhitungannya :
Luas persegi besar = Luas persegi kecil + 4 Luas segitiga
( b + a ) . ( b + a ) = c . c + 4 . 1/2 b.a
b2 + 2 b.a + a2 = c2 + 2 b.a
b2 + a2 = c2 + 2 b.a – 2 b.a
b2 + a2 = c2
Berdasarkan rumus tersebut terbukti bahwa sisi miring sebuah segitiga
siku – siku adalah akar dari jumlah kuadrat sisi – sisi yang lain.b2 + a2 = c2
—————————————————————
Anda pasti tak asing lagi dengan rumus ini. Rumusnya sebagai berikut:
a2 + b2 = c2a adalah sisi alas (horizontal), b adalah sisi tinggi (vertikal), sedangkan c adalah sisi miring. Untuk lebih jelasnya bisa dilihat pada gambar ini.
Bagaimana? Sudah jelas kan?
Untuk mencari masing-masing sisi digunakan rumus berikut:
Untuk mencari a:Contoh soal:
a = √(c2 - b2)
Untuk mencari b:
b = √(c2 - a2)
Untuk mencari c:
c = √(a2 + b2)
Sebuah segitiga siku-siku dengan sisi alas 5 cm dan sisi tinggi 12 cm. Berapakah sisi miringnya?
Jawab:
Diketahui:Contoh soal lainnya:
a = 5 cm
b = 12 cm
Ditanya:
c = ?
Penyelesaian:
c = √(a2 + b2)
c = √(52 + 122)
c = √(25 + 144)
c = √169
c = 13
Jadi, sisi miringnya adalah 13 cm.
Sebuah segitiga siku-siku dengan garis alas 9 cm dan garis miring 15 cm. Berapakah kelilingnya?
Jawab:
Diket:
a = 9 cm
c = 15 cm
Dit:
k = ?
Peny:
Mula-mula, kita harus mencari sisi tinggi (b) dulu.
b = √(c2 - a2)
b = √(152 - 92)
b = √(225 – 81)
b = √144
b = 12
Lalu, karena b sudah ditemukan, maka kita bisa mencari kelilingnya.
k = a + b + c
k = 9 + 12 + 15
k = 36
Jadi, keliling segitiga tersebut adalah 36 cm.
Sumber: http://www.adipedia.com/2011/05/mencari-panjang-sisi-miring-segitiga.html







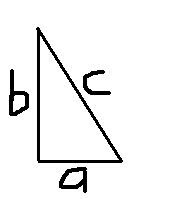











0 komentar:
Posting Komentar